线性回归是一种广泛应用于数据分析领域的统计方法。它用于建立因变量与一个或多个自变量之间的关系。在本文中，我们将详细探讨线性回归的概念，包括它的工作原理、假设以及如何解释结果。我还将提供示例和图表来帮助说明这个概念。

什么是线性回归？

线性回归是一种统计方法，用于确定两个或多个变量之间的关系。特别是，它用于寻找描述因变量与一个或多个自变量之间关系的最佳拟合直线。因变量是被预测或解释的变量，而自变量是用来解释因变量的变量。

在线性回归中，因变量和自变量之间的关系通过 y = mx + b 形式的方程建模，其中 y 是因变量，x 是自变量，m 是斜率线，b 是 y 截距。

直线的斜率表示 x 单位变化时 y 的变化，而 y 截距表示 x 等于零时 y 的值。直线方程可用于根据自变量的值对因变量的值进行预测。

线性回归假设

线性回归对所分析的数据做出若干假设。这些假设是：

1.线性：因变量和自变量之间的关系是线性的。

2. 独立性：观察结果相互独立。

3. 同方差性：误差的方差在自变量的所有值中都是恒定的。

4. 正态性：误差服从均值为零的正态分布。

5.无多重共线性：自变量之间的相关性不高。

如果不满足这些假设，线性回归分析的结果可能无效。

线性回归的例子

广告和销售

假设我们有兴趣研究某种产品的广告支出与销售额之间的关系。我们收集了 10 个不同时间段的广告花费金额和相应销售数据的数据。数据如下表所示：

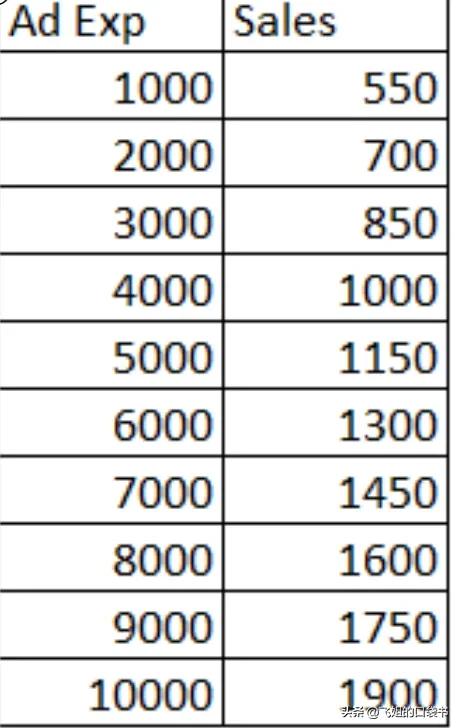
我们可以使用散点图将广告支出与销售额之间的关系可视化，如下所示：

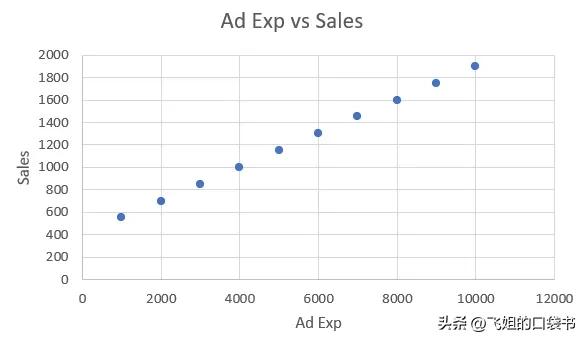
散点图表明广告支出与销售额之间存在正相关关系。随着广告支出的增加，销售额也往往会增加。我们可以使用线性回归找到最能描述这种关系的直线方程。

使用统计软件包，我们获得以下输出：

Coefficients:
             Estimate Std. Error t-value Pr(>|t|)    
(Intercept) -195.0000   139.6779  -1.397    0.197    
AdExpend      0.1950     0.0243   8.016  2.9e-05 ***

输出显示直线的斜率为 0.1950，y 截距为 -195.0000。斜率告诉我们，广告支出每增加一个单位，销售额就会增加 0.1950 个单位。y 截距告诉我们，当广告支出等于零时，销售额等于 -195.0000 单位，在这种情况下这不是一个有意义的值。

我们可以使用直线方程，根据广告花费的金额来预测产品的销量。例如，如果我们在广告上花费 5000 美元，我们可以预测该产品的销售额将是：

Sales = 0.1950 * 5000 - 195.0000 = 805.000

结论

线性回归是分析两个或多个变量之间关系的有用工具。通过对数据拟合一条直线，我们可以确定关系的强度和方向，并根据自变量对因变量进行预测。但是，请务必记住，线性回归对数据做出了某些假设，如果不满足这些假设，则分析结果可能无效。